How would a piano sound on Mars?

Brad MacClure - 23 December 2024

A few weeks ago the following came up as a brief discussion on a facebook group:

So let’s pretend we’re living in the near future and Mars has been colonised.

Some billionaire moves to Mars and decides to bring along a grand piano (let’s say a Steinway B ).

As luck would have it, this billionaire hires YOU to travel to Mars (think of the mileage fee!) and regulate the piano so it plays just as well in Mars’ gravity as it does on earth.

How would you go about regulating that piano? Would it even be possible to make a piano play as well in 38% of earth’s gravity?

(thanks to Andy LaFave for this comment)

Okay, you may have noticed from that last sentence that this question is about “regulating” the piano. To be clear, regulating is not exactly about the sound. It’s more about the mechanics of creating the sound. But the post and discussion got me thinking about the sound as well, so I’m going to discuss that too. We will get to what regulation is about a little later.

In any case, I thought this would be a fun diversion from all my recent horsey nonsense, so let’s have a look at it. There are two main factors to consider: How a piano sounds, and how it plays. How it sounds is mostly about the atmosphere, while how it plays is mostly about gravity.

Sound in a less dense gas medium

Based on information I can glean from the internet, a piano would sound the same in a Martian atmosphere. Much quieter, for sure, and some of the high notes might even get lost entirely, especially over distance, due to the damping effect of the carbon dioxide atmosphere.

Would the pitch be different? You might be tempted to think so, but from what I’ve read I think the answer is no.

The frequency of the note is what gives us the pitch. This is measured in cycles per second, also called Hertz (or Hz). A440 (That’s the A above middle C) on a piano is 440 Hz, for instance. If you take the distance sound travels in one second and divide that distance by its Hertz, that will be the actual wavelength of that note. Here on Earth sound travels at 343 metres per second in average conditions (not always, but for now let’s go with that). So the wavelength of A440 is 343/440 = 779 mm. On Mars, sound travels a bit slower, around 240 m/s. So on Mars A440 would have a wavelength of 545mm. The note’s wavelength shortens in the less dense atmosphere, but because it’s not travelling as fast it would still hit our ears at 440Hz, so the pitch would sound the same to us.

OK, but here’s the weird and different thing: In the Martian atmosphere, higher frequencies travel faster than lower ones. If you’re interested in this, here’s a detailed explanation, but this poses a few real issues for your Martian piano recital. The frequency where the problem starts is 240Hz. (Middle C is 261.63Hz.) So basically your right hand notes will reach your audience before your left hand notes! Treble notes are more than 10 metres per second faster than bass notes in fact. I couldn’t find out whether it’s just one faster speed for all the notes above 240Hz, or if it gets worse as the pitch goes up, but either way this would be just hopeless. So as long as you’re really close to the source, it should be fine, but the further away you get the bigger delay you’d hear on the treble notes. Imagine trying to set up a big concert. You’d have to put the signal through a device (Earthlings call it a “crossover”, but it’d have to be a really complex one) which separates out the frequencies to different signals, then puts a delay on the higher ones, measured to reach the audience at the same time as the lower ones. It would also be different for audience members at different distances!

To make things more complicated, in reality high pitched partials or harmonics exist in the lower notes as well. So at any distance you’ll hear the top notes of the piano plus the “brightness” of the bass strings first, then the low notes. But the low notes would sound muffled, because you’ve already heard the brightness of them a half second ago.

What’s “regulating”?

Regulation is what we call all the adjustments made to the action of a piano (the mechanical bit), with the goal of making it respond properly to the pianist’s playing. Regulation is equally as important as the tuning of the piano. The action contains the keys, the felt hammers which hit the strings, and several complicated interacting moving parts in between that allow for things like escapement, drop, spring, checking, key down weight, key up weight, and so on. Changing any one of those things can affect the others, and the result is a very frustrated concert pianist.

Here’s the problem; the action totally relies on gravity to work properly. There are weights in the keys which balance them, and also contribute to how heavy they feel to press down (we call that “down weight”), how they return (up weight), and the moment of inertia, which is the kinetic energy required to just get the key to move. Then there’s the rest of the action. The hammers have their own weight. They return under gravity, rest on the repetition levers, which have upward spring in them. None of this would work properly in Martian gravity, which is 38% of earth’s gravity. Adding weight clearly wouldn’t work right? Because remember, heavier objects don’t fall faster, they just have more momentum when they land.

Have a look at the diagram below of a grand piano action.

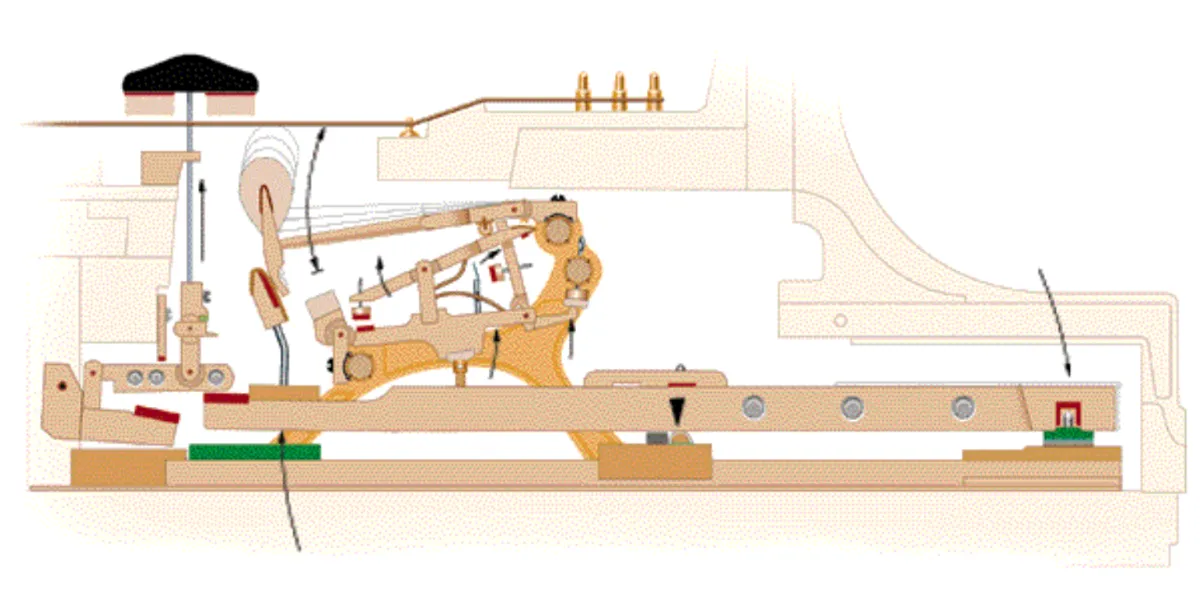
The arrow on the far right is where it all starts, with you pushing down on the key. This would feel lighter than it should, because everything after that is being pushed upward, and of course it would all weigh less because of low gravity. You could add weight to the end of the key, or remove the weights from the front of the key (you can see this key has three lead weights). That might help with keeping the down weight feeling okay, but neither of those things are going to solve the slow return of the action to its resting position. In between the key and the hammer knuckle are the wippen, the jack, and the repetition lever. I won’t spend any time on those, because they’re all regulated with springs, and I think they’d be the least of our worries. The hammer will still have good momentum for hitting the string, and it should bounce downward okay into “check” (that’s the wee thing connected to the left end of the key that looks like a brake that the hammer head is falling onto). Real problems will start, though, when you try to play the same note again rapidly. The hammer needs earth-like gravity to get back down fast, or the note will miss.

There’s also the damper, which drops onto the string when you release the note, or all of them drop at once when you release the pedal. That’s the black thing near the top left in the diagram. It’s also weighted, and would take too long to get back down onto the string, causing notes to “ring on”.

So, how to fix this. How to simulate gravity, the same old question from every science fiction story since 2001. Springs? Play the piano in a giant centrifuge? Magnets?

I think magnets are the way. Although the centrifuge idea sounds cool too. Neodymium magnets are amazing and cheap, and let’s face it, Elon’s probably got all your money now after flying to Mars. You’d position two opposing magnets to repel the hammer back down. You’d need another two to push the damper down, or you might be able to get that done with just one if you’re clever. There are 88 notes and 67 dampers, so 243-odd little neodymium magnets ought to do the trick. I think this would be fun to try. By the way, I’m chuffed that Andy mentions a “Steinway B” in this thought experiment. There’s a Steinway B about 3 metres away from me in my kitchen while I type this. Hmmm…shall we experiment?