How Lumpy is Random? and other burning questions in quantitative reasoning
David Bulger - 1st February 2014
Most people are very bad at distinguishing genuine patterns from random noise, but fortunately there are statistical methods that can help. This article is adapted from a talk at the NZ Skeptics Conference, in Wellington, 7 September 2013.
Statistics is one of those things, like health, politics and home maintenance, that everyone should know a little about. It is important in the life of an informed modern citizen and a major part of scientific literacy.
A narrow definition of numeracy implies proficiency at specialised calculations; a broader notion of it encompasses intuition about quantity and significance, and a general understanding of how statistics works and what statistical claims mean. These concepts are essential for a critical engagement with journalism and public discussion.
For instance, some sense of the scale of very large and small numbers is required to evaluate the plausibility of abiogenesis and the evolution of diverse species by natural selection; the whole theory is absurd if we don’t appreciate the Earth’s immense age and size (especially when compared to the speed of molecular biochemical processes and the size of the relevant molecules and cells). Intuition for significance helps us draw the line between mere coincidence and meaningful patterns when we read a number of anecdotes about vaccinated children developing autism, or see a string of record-breaking storms in the news, or see a cloud bearing a striking resemblance to (Renaissance painters’ depictions of) Jesus. Lastly, a qualitative overview of statistics tells us what kinds of questions statistics can and cannot answer, and how statistical arguments can be used to inform or mislead.
Pareidolia
We don’t have fangs, exoskeletons, camouflage or venom; humans rely on intelligence to survive. A big part of intelligence is pattern recognition, and we’re very good at it. Maybe too good. The human brain does not take an ‘innocent until proven guilty’ approach to looking for patterns; we imagine trends and connections on the slightest whiff of evidence. This kind of over-interpretation of random data is called pareidolia.
Sometimes, we know the perceived patterns are imaginary, and they can even be useful. For example, grouping the stars into constellations sketching out fanciful images aids in learning the arrangement of the night sky - whether or not we believe that Poseidon placed Cassiopeia in the sky as a punishment. But when we don’t know a priori whether perceived patterns are systematic, intuition is a poor guide. One of the main aims of statistics is to provide objective quantitative measures to determine whether apparent patterns are too strong to appear by chance.
Part of the difficulty with intuition is that truly independent random data tends to cluster more than people expect. (Random is lumpy!) For instance, the chance of any two people sharing a birthday is about 1-365, or 0.27 percent. However, this seemingly rather unlikely event probably will happen (with a 50.73 percent chance) in some pair, given a group of only 23 people - but it will still seem like a surprising coincidence.
To test your own intuition for the amount of clustering appearing in independent data, try this this interactive random dots image.
Hypothesis testing
Hypothesis testing is one of the central methods of statistics. Loosely, it is used to quantify the amazingness of a coincidence. When a pattern is perceived, hypothesis testing can be used to distinguish between pareidolia and real systematic trends.
The world is already awash with quantitative, nitty-gritty, formulaic descriptions of the mechanics of hypothesis testing, and I’m not going to add to them (not here, anyway). Instead, let’s focus on the conceptual framework.
Hypothesis testing is all about measuring the consistency between observed data and some hypothesis (called the null hypothesis) about where the data came from. This is done by gauging how extreme the data would be, if the null hypothesis were true. ‘How extreme’ really means ‘How improbable would this data be if the null hypothesis were true?’ or more accurately ‘How likely would we be to see something as extreme as - or more extreme than - the observed data, under the null hypothesis?’
Suppose we make an observation which produces two numbers. We can use these numbers as horizontal and vertical coordinates to plot a point on a graph. If we have a null hypothesis, that is, a theorised mechanism for producing observations, we can use it to produce a large sample of points on the graph; this is shown in Figure 1a as a cloud of grey dots representing hypothetical observations.
Now suppose we make an actual observation, and plot it in black, superimposed on the cloud of hypothetical observations. If it falls comfortably in the middle of the cloud (eg, Point A), then it accords perfectly with the null hypothesis: the grey dots and the observed point may have the same distribution. On the other hand, if it falls well outside the cloud (Point C), then it is not the kind of point produced by the hypothesis; we have strong evidence against the hypothesis.
But where do we draw the line? If the observed point falls just on the outskirts of the grey cloud (Point B), it can be difficult to judge how consistent it is with the hypothesis. Mathematics (or, often nowadays, computer simulation) can be used to calculate how extreme the observed point is with respect to the grey distribution. Conventionally, if the observed point falls in the outer five percent of the grey cloud, the null hypothesis is rejected. (This threshold, five percent, is called the significance of the test. It describes how much evidence against our null hypothesis we will need to see to persuade ourselves to reject it.) Figure 1b shows a decision boundary separating the most extreme five percent of the null distribution from the most typical 95 percent.
Figure 1
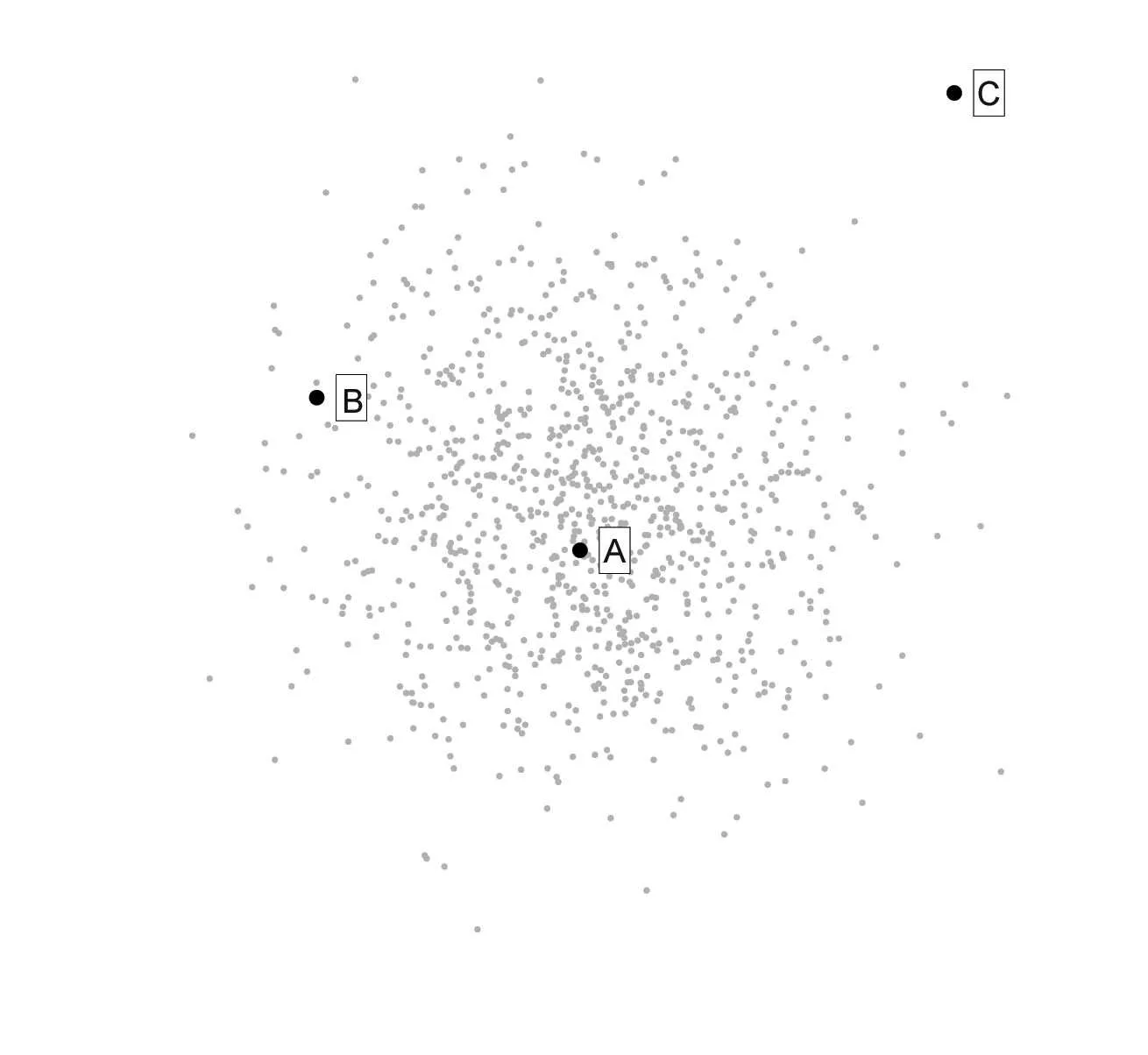
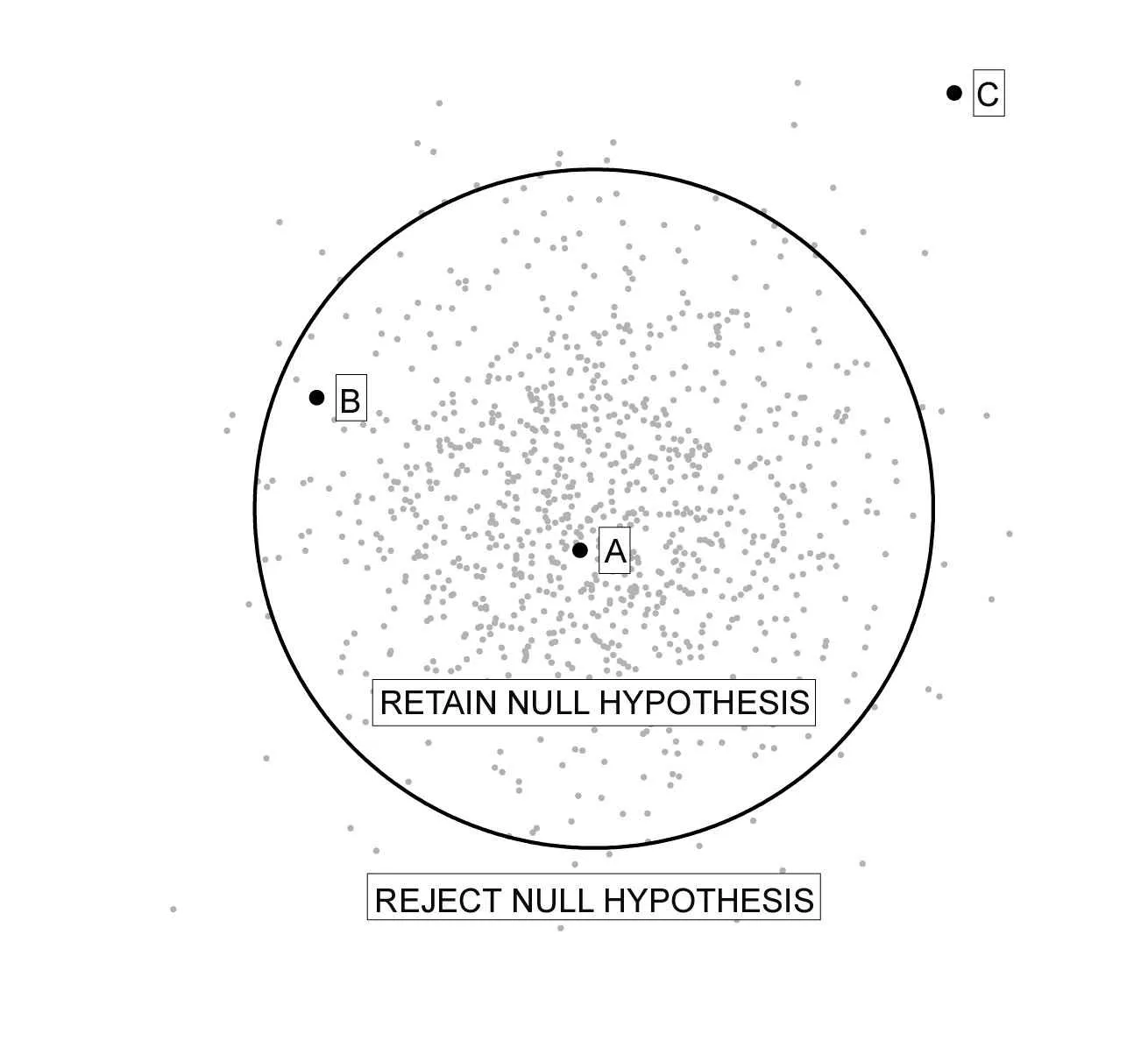
This conceptual framework has some implications. Firstly, the null hypothesis needs to be a specific, falsifiable hypothesis, and therefore usually states that some variable, medical intervention, et cetera has no effect on some outcome. Also, there is no such thing as evidence for the null hypothesis, only evidence against it; the question is whether there is enough evidence. If the null hypothesis is nearly but not quite true, e.g., if there is a small but systematic relationship between two variables, then a hypothesis test based on a small sample will be unlikely to find the relationship, whereas a large enough sample will find it. So if a study retains the null hypothesis, it means one of three things: too little data was used, or there is no relationship, or there is a relationship but we tested for the wrong kind of relationship. And even if there is no relationship, the significance level (also known as the false positive rate) gives the probability of wrongly rejecting the null hypothesis, so that typically 1 in 20 studies will find a non-existent relationship.
Let’s consider the danger of searching for the wrong kind of relationship in more detail. The ‘answer’ a hypothesis test gives can only be as sophisticated as the question - and generally, more sophisticated questions require more data to answer. For instance, if a study investigates the health effects of a certain food, drug or exercise, usually it only considers the effect on an average subject.
Consider clinical experiments aimed at determining the Recommended Daily Allowance of “Nutrient X.” Presumably, each person actually has a different optimal intake of Nutrient X, so if we give everyone the same dosage, it will be a little too much for some people, and not quite enough for others. With a large enough sample, we might even be able to determine which other variables influence each subject’s optimal intake. However, it requires more data to study the combined effect of Nutrient X and daily exercise, say, than the effect of Nutrient X alone, and data sets are never as large as we might like. Estimating only the average optimal intake of Nutrient X is a compromise, and suits almost no one perfectly. If the RDA has been 250 mg-d, and a new study indicates that it should be raised to 300 mg-d, that may increase average health, but it will at least slightly decrease the health of almost half the population! Try this yourself HREF=“http://www.skeptics.org.nz/RDANutX”>below.
Statistics in journalism
In preparing to present this material at the NZ Skeptics conference in Wellington this year, I wanted to illustrate statistics’ place in daily life by finding a newspaper piece reporting on a scientific study, tracing it back to the original journal article, and looking at the statistical methods involved and how they were presented in the newspaper. The very first science piece I found was www.stuff.co.nz-science-9088473-Kiwifruits-surprising-health-benefits, reporting on a study conducted at Otago University on kiwifruit’s effect on health.
Credulously reading the newspaper piece, we learn that “good things can happen when normally fruit-and-vegetable-averse university students eat two kiwifruit a day.” The piece indicates that, during the six-week study, the two halves of the sample group ate either two kiwifruit, or half a kiwifruit, per day. The two-kiwifruit group showed significantly less fatigue and depression than the other group. The piece also mentions that the study was partly funded by Zespri International; this shouldn’t necessarily prejudice us - nutritional research on kiwifruit seems an appropriate thing for Zespri to spend money on - but obviously it raises the possibility of biased or perfunctory work.
The original journal article, “Mood improvement in young adult males following supplementation with gold kiwifruit, a high-vitamin C food” by Carr et al., had recently appeared in the Journal of Nutritional Science, and naturally goes into a lot more detail about the study. It explains that the sample comprised 36 male university students, selected after some screening. Smokers were excluded, as were excessive drinkers, diabetics and anyone with a bleeding disorder or kiwifruit allergy or on prescription medication; there may be good reasons for these exclusions, though (particularly for young adult males) is the sample still representative of the population? However, the remaining exclusions are where, for me, the story started to unravel. The study also excluded anyone with high fruit and vegetable consumption, anyone taking vitamin C supplements, and anyone with average or higher blood plasma concentration of vitamin C. The article’s study design section explains that, during the six-week observation period and for five weeks prior, the subjects were instructed to keep to a diet low in vitamin C. That is, the researchers deliberately narrowed the experimental sample to subjects who already had low vitamin C, and ensured that they continued to get too little vitamin C other than via kiwifruit. It turns out that two kiwifruit per day is healthier than half a kiwifruit per day - when kiwifruit is given a monopoly over your vitamin C intake. The newspaper piece mentions nothing about the exclusions or restricted diet. The journal article’s conclusion is much fairer: “Overall, our kiwifruit supplementation study shows that a positive effect on mood and vigour can be measured in an otherwise well population with suboptimal intakes of fruit and vegetables and vitamin C.” It is tempting to imagine that news originating from the objective disciplines of science and statistics can be trusted. Unfortunately, it is easy for the interpretation of such work to be distorted, due to conscious or unconscious bias, sloppiness, or simply word count pressure. Often, the distortions in journalism and other public discussion can only be guessed at, but a general awareness of the common sorts of misrepresentations, at least, is helpful. The peculiar geometry of multi-dimensional data Figure 1 depicts two-dimensional data: each observation produces two numbers, and by using these as coordinates, we can plot the observations in a two-dimensional graph. Using perspective, 3D glasses or solid models, we can depict three-dimensional data in a similar way. Because we live in a universe with only three spatial dimensions, we cannot use the same graphical methods for higher-dimensional data, but of course many studies involve observations which each produce many more than three values. High-dimensional data has some counterintuitive geometrical properties. In fact, even two-dimensional data sometimes confounds our intuition. From time to time, one hears driving ability used as the classic illustration of the cognitive bias known as illusory superiority, people’s tendency to overestimate their abilities and qualities relative to others’. Over the years, several studies in various countries have found that most people surveyed consider themselves to be above-average drivers. It is then pointed out that it’s not possible for most people to be better than average - and this seems reasonable (if ‘average’ means ‘median’ anyway). The seemingly inescapable conclusion is that a lot of people overestimate their driving ability. That most people overestimate their driving ability should be obvious to anyone who’s ever been in a car - or near a road. (And kiwifruit probably are quite good for you!) But this is not implied by the survey results, because what constitutes ‘driving ability’ is subjective and multi-dimensional. Many qualities are involved in driving ability. To keep things simple, suppose that driving ability encompasses just ‘skill’ and ‘caution’, and that everyone agrees how to measure skill and caution, but that opinions vary on the relative importance of skill and caution. Probably most drivers will put more effort into developing the qualities they rate as more important, whether skill or caution. So most drivers will be, subjectively, above average - with no self-deception. For help visualising this, try this interactive driving ability graph. [AboveAverageDrivers.html goes here] In fact, driving ability comprises many more than two dimensions, strongly accentuating this effect. Almost any driver will be above average in some qualities, and below average in others. We can expect that drivers will tend to overvalue their strong points, and undervalue their weak points, for two reasons: drivers will work harder to learn habits they value, and ‘sour grapes’ (drivers will eventually dismiss things they can’t master). Our initial idea - that most drivers’ considering themselves above average implied widespread overconfidence - was flawed, because it assumed dimension reduction to be trivial and objective. Statistics has been described as ‘the language of science’, because of its focus on testing for disagreement between data and theory. Some familiarity with statistics, and numeracy in general, makes for a more informed and engaged public. David Bulger is a senior lecturer in the Statistics Department at Sydney’s Macquarie University. As well as maths and computing, he has a misguided inclination for playing and writing music. Caption for Figure 1: Figure 1. In (a), the grey cloud represents the null distribution, a theory about the distribution the observed data should follow. If we observe A, the theory seems reasonable. If we observe C, the theory seems unreasonable. But it is less obvious whether an observation of B significantly contradicts the theory. In (b), we separate the most typical 95% of the null distribution from its most extreme 5%; since B sits within the most typical 95%, we conclude that it agrees with the theory.