Playing the numbers game
Jay D. Mann - 1st November 2007
Some risks in life are distributed throughout a population, others are all-or-nothing. There’s a big difference. This article is based on a presentation to last year’s Skeptics Conference.
Many organisations, not excluding certain government agencies, rely heavily on public fear to influence public decisions and to provide their on-going funding. That provides strong motivation to generate fake fears even where there is no real public danger.
There are several methods in use:
-
The distinction between evenly distributed risks versus all-or-nothing risk is obscured.
-
Forecasts that should be written as fractions, are multiplied, unjustifiably, into a purported risk to individuals (“10 deaths per million”).
-
An obscure statistical trick is used to treat the most extreme possibility as though it is the most likely.
-
Numbers are reported with unjustifiable levels of precision to provide a reassuring air of scientific competency. A check of your foods cupboard will reveal boxes claiming, say, 798 mg of protein, where natural variations in ingredient composition can justify only “0.8 g”.
Kinds of risks
Imagine that a maniac injected a lethal dose of undetectable poison into one orange in a box of 1000 fruit. Would you willingly eat an orange from that box? Surely the risk of dying is more important than the minor pleasure of a juicy fruit.
On the other hand, assume that these 1000 fruits are converted into juice. Everyone who drinks a portion of juice will ingest one-thousandth of a lethal dose. Aside from the yuk-factor, would you drink this beverage? I would, since a dose of 0.001 of the lethal dose will not, in the absence of any other negative factors, harm me. A critical enzyme that is blocked by 0.1 percent will still provide 99.9 percent functionality. In fact, most enzyme systems are down-regulated (throttled back) by our natural feedback controls. We routinely consume significant but harmless amounts of natural poisons such as cyanide. Our bodies are rugged; we are not delicate mechanisms. We can function despite losing half our lungs, half our kidneys, most of our liver, and even parts of our brains. Most critical parts of metabolism are backed up by duplicate mechanisms. The key term here is ‘biological threshold’. To speak of a ‘low dose of poison’ is to mouth a meaningless collection of sounds: only high doses of poisons are poisonous. Evenly distributed risk versus all-or-nothing distribution
Returning to my example of the poisoned oranges, the risk factor is one in a thousand for an individual fruit and for a glass of juice. The difference between the two is that risk is lumped all-or-nothing in one case, and distributed uniformly in the other case. The maths may be the same but the practical conclusions are different.
Here is another example: the Bonus Bond Lottery. My $10 bond receives four percent interest a year, 40 cents annually, about three cents per month. Please don’t clutter my letter box with bank statements reporting another three cents! No Bonus Bond holder wants his or her earnings to be distributed uniformly. Obligingly, the bank turns all these tiny individual earnings into a single monthly prize of $300,000 going to just one lucky person. Three cents is trivial, but $300,000 is life-changing. No wonder people hold onto Bonus Bonds.
Injury from damaging chemicals or conditions is not random
The standard way to evaluate toxicity is to treat a number of animals with increasing amounts of chemical (or radiation, etc). The LD50 is the dosage where half the animals die (or develop cancer, etc.) Is the LD50 an example of all-or-nothing risk? In fact, it is a distributed risk applied over a heterogeneous population. All the animals given the LD50 dose were seriously ill but only half of them succumbed. Perhaps they had been fighting, or simply were genetically weaker. It’s hard to tell. Presumably the healthiest animals were most likely to survive.
Examine a lower dosage, where only 10 percent of the animals succumbed. The survivors didn’t go off to play golf! All were affected, but one in 10 was too weak to survive. If you imagine a bell-shaped curve where ‘health’ is on the x-axis, then a low dosage shifts all the animals to the left; those who started on the low-health side of the curve were likely to drop off the mortality cliff.
We can apply this logic to episodes of severe air pollution. We can predict, in advance, who is likely to die and who is likely to survive. There might be, say, 20 deaths per 100,000, but that does not mean an otherwise healthy man or woman has 20 chances in 100,000 of dying. It’s the people with pre-existing respiratory problems who are at risk, not everyone.
Groups that forecast a certain number of deaths per million, from a particular environmental contaminant, should be challenged to describe in advance the characteristics of the victims. Purported victims of tiny doses of chemicals will be abnormally inept at detoxification, perhaps because of liver disease. They are probably hypersensitive to many chemicals in addition to one particular man-made chemical. One may wonder how such people have survived to adulthood.
Turning 100 rats into millions of people
The rules for long-term testing of potential carcinogens are:
-
100 rodents per concentration (x 2 for both males and females).
-
At least three dose levels.
-
Highest dose levels such that animal growth is inhibited about five or 10 percent (ie, partly toxic doses).
-
Lowest dose is one-tenth of highest. (Very narrow range).
-
Attempt to minimise number of animals for both humanitarian and economic reasons (US$600,000 per study).
Successful experiments are those where, at high doses, death or cancer rates of 10 to 90 percent occur. For statistical and practical reasons, responses below 10 percent are difficult to measure. (A massive $3 million ‘mega-mouse’ effort failed to confirm a forecast of one percent cancer caused by low levels of a known carcinogen.) So estimates for risk at low doses can only be done by extrapolating high-dose results.
There are different ways to calculate hypothetical response to doses lower than tested. These are:
- quadratic
- linear
- power
- non-linear transition
- threshold
Do we really care which extrapolation equation is used? Arguments between log-linear, probit, or threshold models are no better than discussions about whether the angels dancing on the head of a pin are doing the waltz or the two-step. It’s the unjustified extrapolation that’s at fault.
Remember, the number of rodents used is in the hundreds. Extrapolations give rise to predictions of, say, 0.001 cancers per 100 rats at a certain dosage. The meaning of this number is obscure. What is one-thousandth of a cancer?
Obedient computers, run by scientific spin doctors, multiply the numbers by 1000. So now the prediction is one cancer per 100,000 rats. Better yet, “10 cancers per million rats”, or perhaps “9.8 cancers per million”, to simulate spurious precision. We can now perform the brainless arithmetic of multiplying “10 per million” by the population of New Zealand, resulting in newspaper headlines of “40 cancer cases” per year. All this from fewer than one thousand rats!
Something is seriously wrong with this approach to toxicity testing. It predicts, with unjustifiable precision, death or cancer rates that are forever unverifiable. Moreover, high-dose tests can overwhelm natural defences, falsely suggesting damage from lower doses, damage that is never observed.
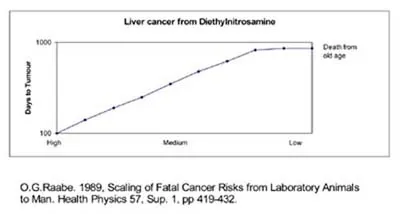
An alternative way to handle toxicological data is to see how long it takes for chronic doses to cause damage. An important paper by Raabe (1989) did this for both a chemical carcinogen and for radiation damage. His plots show, logically, that as the dosage was lowered, the animals survived longer. In fact, at low doses the animals died of old age!
Toxicologists using this approach could estimate “time-to-damage” with considerable reliability. (Converting rodent risk to human risk would remain problematical.) The results would be reported as, for example, “At this low dosage, our data predict onset of cancer in individuals with more than three centuries of exposure at the permitted level.” This kind of reassuring forecast would not, unfortunately, inspire larger budgets for the testing agency.
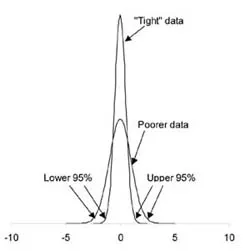
The ‘upper boundary scam’
The bell-shaped normal curve offers another way to fool the public. At the standard threshold of ‘95 percent confidence level’, there is an upper limit point and a corresponding lower limit point. We expect the ‘real answer’ to lie between those points, but the most likely value is around the middle of the range. An honest report of our results should include both the mean (middle) value together with some indication of how broad our estimate is.
I have a homoeopathic weight-loss elixir to market. I have run simulated tests on 30 women using Resampling Statistics. (This is a low-budget business and I don’t want to waste my advertising budget on real experiments.) The mean result was, of course, zero change, but there was an upper-bound of 2 kg weight loss. (There was also a corresponding figure of minus 2 kg weight loss, ie, gain, but we won’t worry about that!).
Am I entitled to advertise ‘Lose up to 2 kg’? After all, 2 kg loss was a possibility, even though it’s right at the edge of statistical believability. My proposed advertisement is sharp practice, probably fraudulent. Surely no reputable organisation would distort their results this way!
Such considerations do not seem to bother US and NZ environmental agencies, which happily quote ‘upper bound’ forecasts. The US Environmental Protection Agency (EPA) wrote:
“We were quite certain any actual risk would not exceed that [upper bound] and would be a very conservative application and be quite protective. It does not necessarily have scientific basis, but rather a regulatory basis… EPA considers the use of the upper 95 percentile as a conservative estimate.”
Problems
One problem with the upper bound estimate of risk is that the worse the underlying data, the more extreme the upper bound, and hence the greater the forecast risk! Some people might think this might motivate the EPA not to refine and expand its experimental database, but I couldn’t possibly comment.
There is nothing inherently wrong with using the upper bound; it does indeed offer reasonable confidence that no damage will occur. But it is dishonest if the central prediction, the mean (average) is not also given. The difference between the mean and the upper-bound tells the public whether or not the estimates are too crude to believe. Unfortunately both numbers are rarely given. One EPA spokesman stated that “The upper bound and maximum dose estimate is usually within two orders of magnitude” (my italics).
That’s an error margin of 100-fold!
A revealing example of how this works was given by EPA in a now-defunct web page devoted to estimating risks from chlorine residues in swimming pool water. That page seems to have been withdrawn, but my own copy of it is at www.saferfoods.co.nz/EPA_drinking_water.html
This amazing document considered the health risk if drinking water were contaminated by swimming pool water. The upper-bound risk was 24 bladder cancer cases per year (for the entire American population). Precautions against this happening would cost $701 million (note the convincing precision here). This would save $45 million of medical and other losses. Many people would have considered that such poor payback would be sufficient reason to drop the proposal.
The “24 cases” of bladder cancer represented the upper-bound estimate. The most likely estimate was, however, 0.2 cases per year. This agrees with their admission of 100-fold discrepancy between upper-bound and most-likely. The most likely outcome of spending $700 million would be to avert one case of bladder cancer every five years! Is that what EPA considers “conservative” and “protective”? Incidentally, the US has more than 60 thousand new cases of bladder cancer every year. An effective anti-smoking campaign would halve that number. What the EPA described as a “conservative” approach turns out to be a proposal to waste millions of dollars for little or no benefit.
There is a further consequence of the EPA mathematics. Since low doses of toxins can sometimes improve health (‘hormesis’), EPA’s figures imply a lower-bound estimate that two dozen cases of bladder cancer could be prevented by drinking dilute swimming pool water.
When the American Council on Science and Health petitioned the EPA to eliminate ‘junk science’ from its administrative process, EPA eventually announced that “Risk Assessment Guidelines are not statements of scientific fact … but merely statements of EPA policy.”
We might expect such behaviour from the EPA. After all, it has 18 thousand employees and a budget of more than US$6 billion. You don’t get that kind of money by telling the American public that they need not worry.
Meanwhile in NZ…
Surely our New Zealand government agencies won’t stoop to the dubious flim-flam of the EPA? Consider the NZ Ministry for the Environment report entitled in part, “Evaluation of the toxicity of dioxins … a health risk appraisal”.
www.mfe.govt.nz/publications/hazardous/dioxin-evaluation-feb01.pdf
“The current appraisal has estimated that the upper bound lifetime risk for background intake of dioxin-like compounds for the New Zealand population may exceed one additional cancer per 1000 individuals.
This cancer risk estimate is 100 times higher than the value of 1 in 100,000 often used in New Zealand to regulate carcinogenic exposure from environmental sources. Of course, if there were a threshold above current exposures the actual risks would be zero. Alternatively, they could lie in a range from zero to the estimate of 1 in 1000 or more.”
This confusing prose says, I think, that the likelihood of risk from dioxin-like compounds is much less than one per 1000. It might be zero, but the Ministry has not provided enough vitally important data. Should public policy be made on the basis of unlikely, unprovable, worst-case guestimates?
The upper boundary scam is, I believe, a despicable misapplication of ‘science’. It’s junk science. Should a government agency be allowed to misinterpret data in a way that would lead of a false-advertising claim if tried on by private merchandisers? I think not.
Our brains are not wired to handle low probabilities. We jump to conclusions on the basis of inadequate information. It’s in our genes. Cave men or women who waited around for more information were eaten by sabre-tooth tigers and didn’t pass their cautionary genes on to us. The cave woman who ran at the slightest unusual sound or smell passed her quick-to-act genes on to us. This is not a good recipe for evaluating subtle statistical issues.
In today’s world, there are many people and organisations ready to push their narrow point of view. We need to be as suspicious about groups claiming to ‘protect’ us or the Earth as we are about time-share salesmen and politicians.